

Hope you are able to calculate the integral by yourself. On further simplifying we will get the distance as s = 162.583 m If s ( t) is distance traveled from 0 to t and v ( t) is a velocity for moment of time t, then relations between them may be described as follows: v ( t) d s ( t) d t s ( t) 0 t v ( T) d T So if you have v ( t), you should integrate it by t to get s ( t). Substituting the input values in the formula to find distance we have the equation as follows We know the formula to calculate distance is s = vΓéÇt + (1/2)gt²
#Distance traveled physics calculator free
Substituting the input values we have the equation as suchįind the free fall distance the body has traveled if the time taken by a body is 5 sec, and has an initial velocity of 8 m/s We have to convert 300 km/h to m/s as time is in seconds. We know the formula to find the free fall speed v = vΓéÇ + gt Calculate the free fall speed just before hitting the ground? It takes 8 sec to travel and hit the ground back. If an object is thrown with an initial velocity of 6 m/s.
#Distance traveled physics calculator how to
Note that neither the haversine formula nor Lambert's formula provides an exact distance because it is not possible to account for every irregularity on the surface of the Earth.Use the simple example over here to understand how to use the free fall formula if you are still confused. In the expressions above, β 1 and β 1 are reduced latitudes using the equation below: Where a is the equatorial radius of the ellipsoid (in this case the Earth), σ is the central angle in radians between the points of latitude and longitude (found using a method such as the haversine formula), f is the flattening of the Earth, and X and Y are expanded below. When used to approximate the Earth and calculate the distance on the Earth surface, it has an accuracy on the order of 10 meters over thousands of kilometers, which is more precise than the haversine formula. Lambert's formula (the formula used by the calculators above) is the method used to calculate the shortest distance along the surface of an ellipsoid. Because of this, Lambert's formula (an ellipsoidal-surface formula), more precisely approximates the surface of the Earth than the haversine formula (a spherical-surface formula) can. Results using the haversine formula may have an error of up to 0.5% because the Earth is not a perfect sphere, but an ellipsoid with a radius of 6,378 km (3,963 mi) at the equator and a radius of 6,357 km (3,950 mi) at a pole. In addition, because the velocity is constant 213 at 3, we know that if3 s (t) 3t, then s 0 (t) 3, so s (t) 3t is.

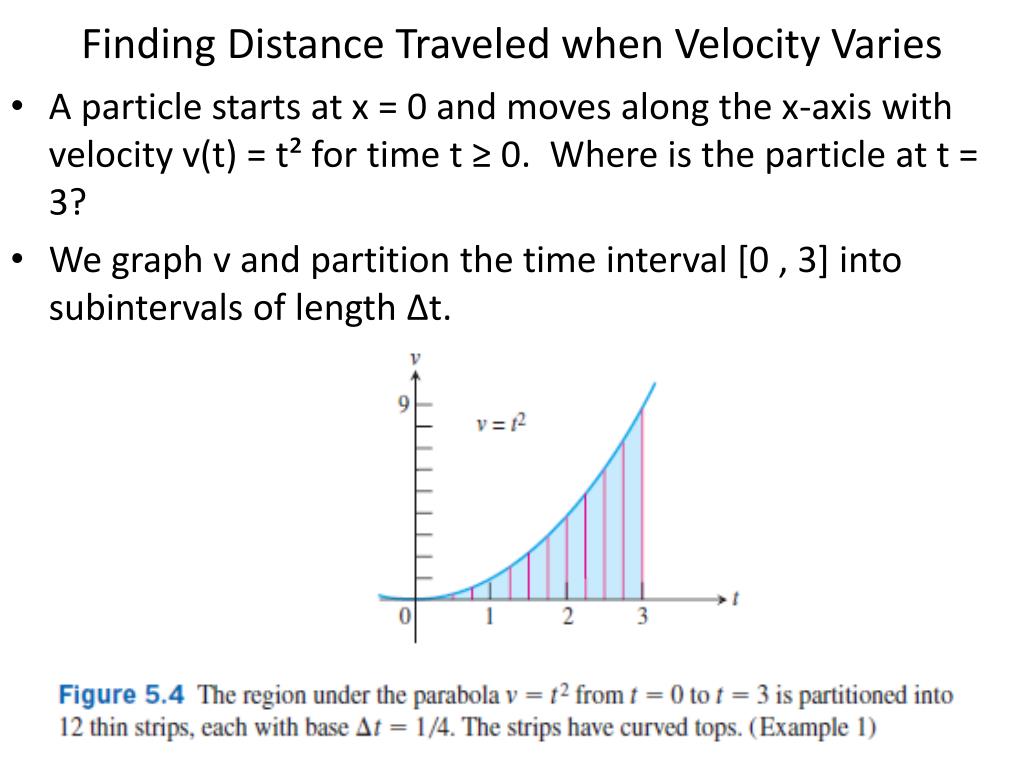
Figure 4.5, we see the already noted relationship between area and distance traveled on the left-hand graph of the velocity function.

The great-circle distance is the shortest distance between two points along the surface of a sphere. Figure 4.5: The velocity function v (t) 3 and corresponding position function s (t) 3t. It is formed by the intersection of a plane and the sphere through the center point of the sphere. A great circle (also orthodrome) of a sphere is the largest circle that can be drawn on any given sphere. The haversine formula works by finding the great-circle distance between points of latitude and longitude on a sphere, which can be used to approximate distance on the Earth (since it is mostly spherical). In the haversine formula, d is the distance between two points along a great circle, r is the radius of the sphere, ϕ 1 and ϕ 2 are the latitudes of the two points, and λ 1 and λ 2 are the longitudes of the two points, all in radians. The haversine formula can be used to find the distance between two points on a sphere given their latitude and longitude: There are a number of ways to find the distance between two points along the Earth's surface. Given the two points (1, 3, 7) and (2, 4, 8), the distance between the points can be found as follows: d =ĭistance between two points on Earth's surface Like the 2D version of the formula, it does not matter which of two points is designated (x 1, y 1, z 1) or (x 2, y 2, z 2), as long as the corresponding points are used in the formula. Where (x 1, y 1, z 1) and (x 2, y 2, z 2) are the 3D coordinates of the two points involved. The distance between two points on a 3D coordinate plane can be found using the following distance formulaĭ = √ (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2 For example, given the two points (1, 5) and (3, 2), either 3 or 1 could be designated as x 1 or x 2 as long as the corresponding y-values are used: The order of the points does not matter for the formula as long as the points chosen are consistent. Where (x 1, y 1) and (x 2, y 2) are the coordinates of the two points involved. The distance between two points on a 2D coordinate plane can be found using the following distance formula


 0 kommentar(er)
0 kommentar(er)
